Física para Bachillerato: 2011

Ondas. Segunda parte.

Ondas en una cuerda

¿Qué sucede cuando una onda llega al otro extremo de la cuerda?

a) Con dos extremos fijos:

Consideremos una onda incidente que se dirige hacia la derecha y choca contra el soporte fijo. Luego del choque, regresa hacia la izquierda. Este cambio en la dirección de la propagación se denomina reflexión de una onda, y en este proceso la onda que regresa se denomina onda reflejada.
En este fenómeno se observa que la onda incidente y la onda reflejada están invertidas una con respecto a la otra y tienen: la misma velocidad de propagación, la misma frecuencia y la misma amplitud.

Onda que se propaga hacia el extremo fijo de la cuerda.

b) Con un extremo fijo (izquierda) y uno libre (derecho):

Supongamos que el extremo de la cuerda esta unido idealmente a un anillo que puede desplazarse sin fricción a lo largo de la barra. Se observa que la onda se refleja sin invertirse conservando además su forma y su velocidad de propagación.

Si la reflexión ocurre cuando el extremo de la cuerda esta libre, la onda reflejada no se invierte.

¿ Y cuando la cuerda está unida al extremo de una cuerda más pesada?

Onda que viaja hacia la derecha por una cuerda ligera atada a una cuerda más pesada.

La dirección de propagación de la onda es de izquierda a derecha, o sea de la cuerda liviana hacia la cuerda pesada . Cuando la onda incidente llega al punto donde se unen las dos cuerdas (separación de los dos medios, donde la cuerda liviana corresponde al medio menos denso y la cuerda pesada como medio más denso); se observa que parte de la onda se refleja y parte se transmite. Tanto la amplitud de la onda reflejada como la amplitud de la onda transmitida son menores que la amplitud de la onda incidente. La onda reflejada conserva su velocidad mientras que la transmitida tienen una velocidad de propagación que depende de la naturaleza del medio. La onda reflejada tienen un cambio de fase de 180ª (se invierte) mientras que la transmitida no tiene cambio de fase.

¿ Y cuando la cuerda está unida al extremo de una cuerda más liviana?

Onda que viaja hacia la drecha por una cuerda pesada unida a una cuerda ligera o liviana

Este caso corresponde cuando una onda pasa de un medio más denso a un medio menos denso. Se observa que parte de la onda incidente se transmite y parte es reflejada; la onda reflejada no se invierte; las amplitudes de las ondas reflejada y transmitida son diferentes a la de la onda incidente. La velocidad de la onda transmitida dependerá del medio de propagación, en tanto que la velocidad de la onda reflejada no varía por propagarse en el mismo medio.

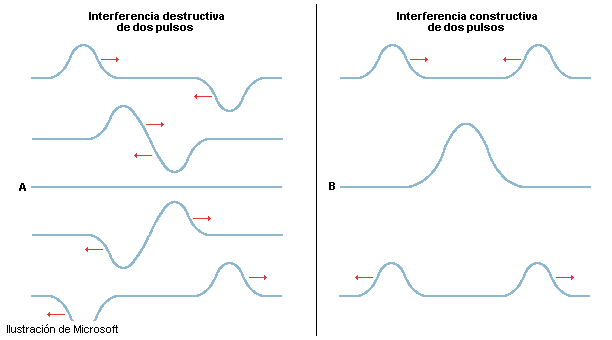
Interferencia

Entrar a:

http://perso.wanadoo.es/oyederra/2btf/609.htm

Título

Pulsos. Principio de superposición (1)

Pulsos. Principio de superposición (2)

Ejercicios resueltos:

Ondas Estacionarias

Ondas Estacionarias

Representación de los diferentes armónicos

Un ejemplo: ocurrió en Tacoma en 1940

Entrar a estas direcciones. Mirar los simuladores.

http://www.ehu.es/acustica/bachillerato/suones/suones.html

http://web.educastur.princast.es/proyectos/jimena/pj_franciscga/reflect.swf

http://www.walter-fendt.de/ph14s/stwaverefl.htm

Algunos ejercicios resueltos:

Ondas. Primera Parte

Ecuación de la onda

Ingresa a este enlace:

http://concurso.cnice.mec.es/cnice2005/56_ondas/index.htm

Algunos problemas resueltos

Ejercicios tipo escrito del MAS

Los siguientes ejercicios son similares a los que aparecerán en el escrito. Recuerda que puedes tener una hoja con las ecuaciones pero no con las gráficas. Suerte y nos vemos.....

Ejercicio de repaso general. Los del escrito son mucho más cortos.

U n cuerpo de 0.25 kg está sometido a una fuerza elástica de constante 25 N/m , se lo aleja 0.30 m de su posición de equilibrio dejándolo oscilar libremente sobre una superficie horizontal lisa. Considere como instante inicial el momento en el que el cuerpo pasa por la posición de equilibrio moviéndose hacia la izquierda.
a) Determinar la amplitud,el período, la frecuencia, la frecuencia angular y la fase inicial.
b) Plantear las ecuaciones de elongación, velocidad y aceleración con sus respectivas gráficas en función del tiempo.
c) Indicar la ecuación de la fuerza restauradora en función del tiempo y graficar en función del tiempo y en función de la elongación.
d) Escribir las ecuaciones de energía potencial elástica,cinética y mecánica en función del tiempo. Graficar en función del tiempo y en función de la elongación.
e) Cuánto vale la energía potencial elástica en el instante en que el cuerpo está ubicado a una distancia igual a la mitad de la amplitud?
f) Dónde está ubicado el cuerpo cuando la energía cinética y potencial son iguales?
g) Cuál es la velocidad del cuerpo en el punto medio de su trayectoria?
h)Cuánto valdría el ángulo de fase inicial si la aplitud del movimiento es ahora 15 cm, e inicialmente el cuerpo está a7.5 cm de la posición central moviéndose con una velocidad inicial negativa?

Tipo escrito:

1) Un cuerpo de 0.200 kg unida a un resorte se mueve con MAS sobre una mesa sin rozamiento. La frecuencia angular es de 8.00 1/s. En el instante inicial el alargamiento del resorte es de 4.00 cm respecto a la posición de equilibrio, y el cuerpo tiene en ese instante una velocidad de - 0.20 m/s. Determinar: a) La amplitud y la fase inicial del movimiento. b) La constante elástica del resorte y la energía mecánica del sistema.

2) La posición de un cuerpo que se mueve con MAS está dada por:
x = 4.0 cos(Pi.t + Pi/4.t)
a) Calcular la posición, velocidad y la aceleración al cabo de 1.0 s de iniciado el movimiento.
b) Explicar detalladamente que es el 4.0, Pi, y Pi/4 que aparecen en la ecuación original. Relacionarlo con el MCU
c) Representar vectorialmente las magnitudes calculadas en a)

Movimiento Armónico Simple.Parte C

Fuerza

Estudio dinámico del mas

View more presentations from Adriana González

Estudio dinámico del MAS by Adriana González

Get your own Virtual Classroom

Aclaración importante: La gráfica de F en función de x (la última diapositiva) pasa por el origen.¿Cuánto vale la fuerza si el resorte no está ni estirado ni comprimido, es decir, cuando x vale 0?

Movimiento Armónico Simple. Parte B

En este link encontrarán un simulador para la elongación:

http://perso.wanadoo.es/cpalacio/mas2.htm

Gráficas y ecuaciones de elongción, velocidad y aceleración para un MAS vertical

a) Estas tres gráficas son para el caso particular, es decir que se empieza a estudiar el movimiento del objeto cuando el mismo está en la posición de equilibrio y moviéndose hacia arriba.

ojo!!!! En la ecuación de elongación donde dice x = Asen(wt) debería decir y=Asen(wt)

b) En estas gráficas se especifica su forma según el cuadrante. Notar que las gráficas de elongación y aceleración son opuestas (amarilla y celeste), mientras que la gráfica de velocidad (verde) está corrido el eje un cuadrante con respecto a la de elongación.

Signos y representación de los vectores velocidad y aceleración en distintos instantes

Ejercicios de MAS

Velocidad:

7) A) Escribe la ecuación horaria de velocidad correspondiente al movimiento indicado en el problema 1). B) Construye una tabla de valores calculando las velocidades cada 0.05 s. C) Grafica velocidad en función del tiempo D) Realiza un esquema a escala mostrando que las diferentes velocidades corresponden a las proyecciones de las velocidades de un cuerpo imaginario que se mueve con MCU en sentido antihorario. E) En la parte d) del problema 1 se indican diferentes ecuaciones de elongación en función del tiempo. Plantea para cada una de ellas la ecuación de velocidad en función del tiempo.

8) A) Plantea las ecuaciones de velocidad en función del tiempo para los ejemplos indicados en el problema 3). B) Realiza las gráficas de velocidad en función del tiempo en cada caso.

9) Utilice los datos del problema 4). Grafique velocidad en función del tiempo.

Aceleración:

Realiza lo indicado en los problemas 7), 8) y 9) sustituyendo en la letra la palabra velocidad por aceleración. Numera los problemas con 10, 11 y 12 respectivamente.

Mmmmmmm..............

Movimiento Armónico Simple. Parte A

Elongación:

1) Un cuerpo se mueve con MAS de ecuación: y = 0.070 sen ( 2π t ). Todas las magnitudes están expresadas en el MKS. a) Construye una tabla de valores calculando las diferentes elongaciones cada 0.05 s durante un intervalo de tiempo igual a un período. b) Realiza la gráfica de elongación en función del tiempo. c) Construye un esquema a escala mostrando que las diferentes posiciones del cuerpo corresponden a las proyecciones de un cuerpo imaginario que se mueve con MCU en sentido antihorario. d) Construye las siguientes gráficas en forma cualitativa: 1) y = 0.070 sen (2π t + π/2) 2) y = 0.070 sen (2π t + π) 3) y = 0.070 sen (2π t + 3π/2) 4) y = 0.070 sen (2π t + π/4) 5) y = 0.070 sen (2π t - π/2) 6) y = 0.070 sen (2π t - π) 7) y = 0.070 sen (2π t - 3π/2).

2) Un cuerpo se mueve con MAS cuya gráfica de elongación en función del tiempo es la indicada. A) Interprete dicha gráfica. B) Indique la ecuación de elongación en función del tiempo. c) ¿Cuál es la ubicación del cuerpo a los 0.10 s de haber iniciado su movimiento? ¿y a los 0.60 s ? Represente ambos vectores. D) ¿En qué instantes el cuerpo está separado de su posición de equilibrio 0.050 m?

3) Las gráficas de elongación en función del tiempo corresponden a diferentes cuerpos cuyo movimiento es armónico simple. Determine para cada uno de ellos la ecuación de elongación en función del tiempo.

4) La gráfica indicada corresponde a un cuerpo que se mueve horizontalmente con MAS. A) Determine la ecuación de elongación en función del tiempo. b) Considere dos instantes comprendidos entre T y T/4 s. Calcule para cada uno de ellos la distancia de separación con respecto al equilibrio y represente el vector elongación en ambos casos. C) ¿Cómo sería la gráfica si se considera como posición inicial el instante en que el cuerpo está ubicado en la posición de equilibrio y moviéndose hacia la derecha? Y si se moviera hacia la izquierda ¿cambiaría su respuesta anterior? Justifique e indique la ecuación de elongación en función del tiempo en cada caso.

5) El dibujo corresponde a una foto por destellos que muestra sobre una mesa horizontal lisa, un resorte fijo por un extremo, y un cuerpo asociado a su extremo libre. El mismo es separado de su posición de equilibrio y dejado en libertad, siendo constante el intervalo de tiempo entre destellos e igual a 0.080s. La escala de la foto es 1/5. A) Determinar la amplitud, el período y la frecuencia angular. B) Calcule las elongaciones para los instantes mostrados en la foto y compárelos con los obtenidos al medir. C) Grafique elongación en función del tiempo. d) Considere tres posiciones diferentes y dibuje los vectores que representan la elongación en cada caso.

6) El esquema representa las diferentes posiciones de un cuerpo que se mueve unido a un resorte sobre una superficie lo suficientemente lisa como para considerar despreciable la fuerza de rozamiento. Escribir la ecuación horaria de elongación y graficar.